P13800 [SWERC 2023] Throwing dice 题解

题目大意

Alice 和 Bob 掷出自己的骰子，将骰子显示的点数相加，然后比较总和。总和较大的玩家获胜；如果双方总和相等，则为平局。

Alice 有 $M$ 个公骰子，第 $i$ 个骰子有 $a_i$ 个面。对于每一个骰子，得到每一个面的概率是相等的。Alice 的得分是她所有 $M$ 个骰子显示的数字之和。类似地，Bob 有 $N$ 个公平骰子，第 $i$ 个骰子有 $b_i$ 个面。

Alice 得分严格大于 Bob 的概率为 $\mathbb{P}_A$，而 Bob 得分严格大于 Alice 的概率为 $\mathbb{P}_B$。如果 $\mathbb{P}_A > \mathbb{P}_B$，输出 $\texttt{ALICE}$；如果 $\mathbb{P}_A = \mathbb{P}_B$，输出 $\texttt{TIED}$；如果 $\mathbb{P}_A < \mathbb{P}_B$，输出 $\texttt{BOB}$。

思路

期望 - OI-Wiki

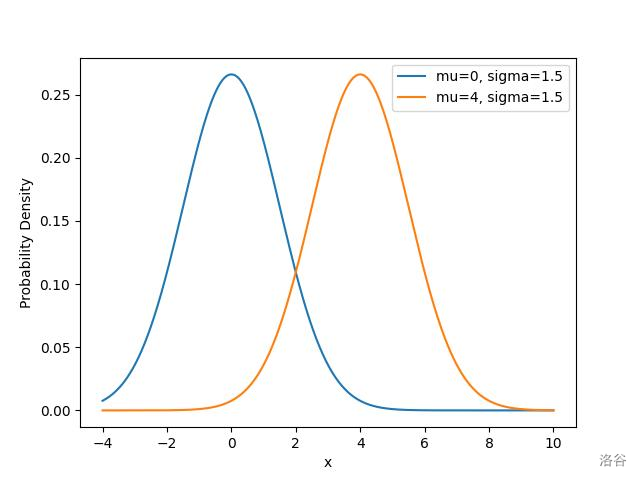
每个骰子的分布是对称的（均匀分布），因此多个骰子总和的分布成正态分布。设 $X$ 为 Alice 的总分数，$Y$ 为 Bob 的总分数，则 $X$ 和 $Y$ 都是对称随机变量。

令 $\delta = E[X] - E[Y]$。由于正态分布：

• 如果 $\delta > 0$，则 $X$ 的分布中心在 $Y$ 的分布中心右侧，因此 $P(X > Y) > P(Y > X)$。
• 如果 $\delta = 0$，则 $P(X > Y) = P(Y > X)$。
• 如果 $\delta < 0$，则 $P(X > Y) < P(Y > X)$。

因此，直接比较总期望值 $E_A$ 和 $E_B$ 即可判断谁获胜概率更大。（题目标签也是期望）

纯暴力写法

通过暴力枚举所有的期望，相加，公式：

$$ \large E_{Alice}=\sum_{i=1}^{m}\sum_{j=1}^{a_i}\frac{j}{a_i} $$

#include <cstdio>
#define MAXN 1000001
int n, m, a[MAXN], b[MAXN];
double Alice, Bob;
int main()
{
    scanf("%d%d", &m, &n);
    for (int i = 1; i <= m; i++)
    {
        scanf("%d", &a[i]);
    }
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &b[i]);
    }
    for (int i = 1; i <= m; i++)
    {
        for (int j = 1; j <= a[i]; j++)
        {
            Alice += j / a[i] * 1.0;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= b[i]; j++)
        {
            Bob += j / b[i] * 1.0;
        }
    }
    if (Alice == Bob)
    {
        printf("TIED");
    }
    else if (Alice > Bob)
    {
        printf("ALICE");
    }
    else
    {
        printf("BOB");
    }
    return 0;
}

时间复杂度：$O(M \cdot max_a +N \cdot max_B)$

会超时，提交记录

空间复杂度：$O(n)$

第一次优化

上文公式可以优化，不难发现第二层循环可以将 $a_i$ 提取出来，即：

$$ \large E_{Alice}=\sum_{i = 1}^{m} \frac{\sum_{j = 1}^{a_i}j}{a_i} $$

将分子替换成求和公式，即

$$ E_{Alice}=\large \sum_{i=1}^{m} \frac{\frac{(1 + a_i) \cdot a_i}{2}}{a_i}=\sum_{i=1}^{m}\frac{(1+a_i) \cdot a_i}{2 \cdot a_i}=\sum_{i=1}^{m}\frac{1+a_i}{2} $$

不难发现，每一次的加法操作只和当前的 $a_i$ 有关，可以将 $a_i$ 数组简化为单个变量

代码如下：

#include <cstdio>
int n, m, a, b;
double Alice, Bob;
int main()
{
    scanf("%d%d", &m, &n);
    for (int i = 1; i <= m; i++)
    {
        scanf("%d", &a);
        Alice += (a + 1.0) / 2.0; // 注意此处的精度问题
    }
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &b);
        Bob += (b + 1.0) / 2.0;
    }
    if (Alice == Bob)
    {
        printf("TIED");
    }
    else if (Alice > Bob)
    {
        printf("ALICE");
    }
    else
    {
        printf("BOB");
    }
    return 0;
}

时间复杂度：$O(n)$

空间复杂度：$O(1)$